数学
全学共通科目として提供されている数学科目は、理系向けと文系向け及び全学向けに分かれている。主要なものについて、その概要を「理系向け」と「文系・全学向け」に分けて説明する。
理系向け
多くの自然科学・応用科学において、数学はその理論を記述するための言葉を提供する。実際、数学無しにはこれらの理論を理解することも正確に記述することもできない。数学は、いわば学問の礎なのである。そこで、理系の多くの学部・学科においては、全学共通科目における数学科目を「専門の基礎となる科目」として必要に応じて幾つか指定し、クラス指定科目として履修を推奨している。ここでは主にこれらの科目について概説する。
クラス指定科目として挙げられる数学科目で多くの学部・学科の学生に関係するものは、次の表にまとめられる。
| (ア) | (イ) | ||
| ① | 微分積分学A・B、線形代数学A・B | 数学基礎IA・B、数学基礎IIA・B |
| ② |
微分積分学続論I・II、線形代数学続論 確率論基礎、数理統計 |
確率論基礎、数理統計 |
|---|
この表は二つの列の科目群 (ア)と(イ) に分かれている。これらは、数学についての一つのカリキュラム(の主要部)をそれぞれ構成している。ある学部・学科は、(ア)にまとめられた科目群の中から履修すべき科目を指定し、別の学部・学科は(イ)の中から指定するなど、学部・学科ごとに決められ、それらは原則クラス指定される。分野ごとに数学の必要性や必要事項が異なるため、その違いに応じて適切に履修ができるよう設計されている。
一方、①・②は学修の順次性を示しており、原則、各列の①の行に書かれている科目を学修してから②の行に書かれている科目を履修することになる。また、学部・学科によっては、②で学修した内容は更なる発展的内容の数学を学修するための基礎事項となる。
数学の学修においては、その順次性は無視しにくい。微分積分の基礎事項の理解も無しに微分方程式(これは微積続論IIで扱われる)を論じようというのは、喩えるなら四則演算も知らずに代数方程式を論じるようなものであり、殆ど意味を成さないであろう。したがって、初期段階の数学の学修を疎かにすると後の学修に悪影響が生じるのは至極当然のことである。各学生においてはこのようなことの無いよう、特に一回生配当の科目については、配当されたクラス指定科目を着実に履修することが強く望まれている。
文系向け・全学向け
文系向け・全学向けに開講されている科目には、例えば以下のものがある。
|
数学基礎A・B[文系]、 文系のための数理統計 |
数学探訪I・II・III・IV |
左側に挙げられている科目は文系向けの科目で、将来の学修で必要となりうる数学的技法を学ぶことを主たる目的とした科目である。現在では、分野によっては文系といえども高校数学の範囲を超えた数学が必要となる。そのような数学的技法を、高校で数学IIIを履修していない学生を対象として講義する。
右側に挙げられている科目は全学向けの科目である。実践的な数学的技法を修得するための科目というよりは、むしろ数学の多様な価値に触れることを目的とした科目である。実際、数学の文化的・社会的側面に光をあてた講義が行われる。
数学科目の紹介 ― 函数の解析を切り口として ―
函数
数学において「函数」(関数)は重要な概念である。函数とは、何かを入力すると数が一つ出力される、そういう装置である。出力される数のことを函数の値と言う。入力するものを動かすとそれに応じて函数の値が動く。函数は変化する量を表わしている。数学では、函数はいろいろな動機を持って研究されている。では、何故函数が興味を持って調べられるようになったのか?それは世の中の多くの「現象」が函数という言葉によって記述されるからである。
「現象を函数で記述する」とはどういうことか?例えば、新幹線に乗って京都から博多に向かうとき、時刻 t における列車の位置を京都からの走行距離として x(t) と表せば、新幹線の走行という現象を函数で記述したことになる。新幹線が一定の速度で走行していれば、x(t) は一次式になり、加速中は下に凸の、減速中は上に凸の函数になる。
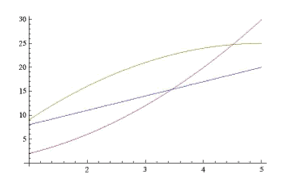 図1 走行距離のグラフ
図1 走行距離のグラフ
他にも例を挙げよう。ある地域の各地点 P に対してそこでの温度 T を対応させれば、これは地点 P の函数を定める。地点 P は座標をつかうことによって2つの変数 x, y で表されるので、温度は2変数函数 T (x, y) で表わされることになる。
温度ではなく、各地点 P での空気の流れ(風)を考えると、それは風向きと強さで表わされる。したがって、風の状態は各点 P に風向きの方向に風の強さに比例した長さの矢印を配置することで表現される (図2)。P = (x, y) を根元とする矢印の、 矢の先端の x 座標の値から x を引いたものを u(x, y) とし、y 座標の値から y を引いたものを v(x, y) で表わすことにすれば、風の状態は (u(x, y), v(x, y)) という2変数 の函数2個の組で表わされる。これもまた函数の仲間であり、2次元ベクトル場と呼ばれる。ベクトル場は「流れ」を記述する際に自然に出てくる。
諸科学において、まず現象を函数で記述し、次にその函数の性質を調べ、最後にそれを現実の現象の下に解釈して理解する、という手続きが、近代以降、基本的・標準的な枠組みとなった。そして、この枠組みの真ん中の部分、「函数の性質を調べる」という部分を、数学が主に担当しているのである。
 図2 ベクトル場
図2 ベクトル場
微分積分とは
数学では函数を調べるために多くの技法が開発されている。全学共通科目として提供される数学科目はこうした技法の基礎を与えている。なかでも微分積分学は中心的な存在である。
微分とは与えられた函数を一次式で近似することである。函数 x(t) を t=t0 で微分することは、変数 t の値が t0 に近いとき(局所的)にもとの函数(複雑なもの)を一次式(簡単なもの)で近似することである。
x(t) - x(t0) ~ c(t - t0)
近似するということを、函数のグラフが表わす曲線を使って言い換えるならば、この一次式のグラフは、曲線上の点 (t0, x(t0)) における接線に他ならない。接線の傾きが t = t0 における微分係数である。微分係数がわかればその函数の t0 の近くでの挙動 ―増加しているのか、減少しているのか― がわかる。微分学は、函数の局所的な振る舞いを調べる。
積分は、函数の大局的な情報を与える。区間での積分(定積分という)は、変数 t が一定の範囲を動く間にその函数が各 t の近くで生み出す寄与を、全て足し上げたものである。例えば、t0 から t1 までの積分の値を t1 - t0 で割ったものはもとの函数の平均値を与える。
微分積分とは、微分と積分を合わせたものであるが、単に「微分と積分」という意味ではない。「微分積分学」という言葉は微分と積分が有機的に関係していることを一言で表している。実際、微分積分学の基本定理と呼ばれる重要な定理があって、それは微分と積分を互いに逆の操作として結びつけるものである。
いま述べたことを、新幹線の走行を例に、具体的現象と結び付けてみよう。函数 x(t) が時刻 t における列車の位置(走行距離)を表すとき、t0 での微分係数 x′(t0) は時刻 t0 での速度である。函数 v(t) = x′(t) は各時刻における速度を表わす。今度は函数v(t)の時刻t = t0 からt = t1 までの積分を考えてみよう。t = t0 からt = t1 までの間の、速度 v(t) の寄与の積み上げとは何を意味するのか?各時刻 t において単位時間当たり v(t) だけ移動するということが速度の意味であるから、その寄与(t の近くでの走行距離)を足し上げて得られる量とは、時刻 t0 から t1 まで間の走行距離 x(t1) - x(t0) である。すなわち、速度の積分で走行距離(すなわち基準点からの位置)が得られる。微分積分学の基本定理は微分と積分を互いの逆として結びつけると述べたが、物体の運動の記述に現れる位置と速度という函数については、位置を微分したら速度が現れ、速度を積分したら位置が得られるという関係になっている。
線形代数とは
線形代数とは、線形性という言葉でとらえられる構造あるいは性質について考察する分野で、線形空間(ベクトル空間とも言う)と線形写像を扱う。
世の中の様々な現象を観察すると、足し算とスカラー倍(実数倍)が自然に考えられる対象がいろんなところに潜んでいることがわかる。例えば、力には向きと強さがあるので、力はベクトルで表わされるが、物体を3つの方向に引っ張ったときに、力が釣り合ったとすれば、3つの引っ張る力は、ベクトルとしての和が 0 になる。
ベクトル場に対して、足し算とスカラー倍を考えることができる。図3の上段のベクトル場を左からθ1, θ2, θ3 と書くと θ1 + θ2 = θ3 である。また、下段はベクトル場 θ3 を3/2倍にしたベクトル場がどうなるかを示している。ベクトルに対して、3/2のような数のことをスカラーと呼ぶ。足し算とスカラー倍からなる構造が線形性であり、 足し算とスカラー倍が定義された集合が線形空間である。
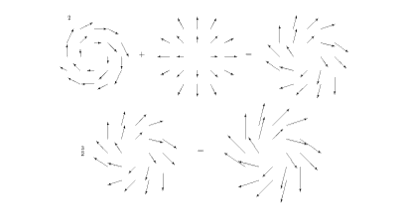
図3ベクトル場の和とスカラー倍
数に対して数を対応させるものが函数であるが、もっと一般に、例えばベクトルに対してベクトルを対応させるときは函数という代わりに写像という言葉を使う。 ここで話題にしたいのは写像の線形性である。写像の線形性とは何か?例えば、平面に原点 O を決め、O を中心に角度 θ の回転を考えよう。回転は平面から平面それ自身への、点を点に移す写像である。平面は原点を決めることによって、2次元ベクトル全体の集合である線形空間 V と同等になるから、回転は V から V への写像を決める。
2次元ベクトル v に対しそれを回転したベクトル を Rθ(v) と書く。この写像はベクトルの足し算とスカラー倍に対して次の性質を持つ。
Rθ(c1v1 + c2v2) = c1Rθ(v1) + c2Rθ(v2)
足し算とスカラー倍を先に行なってから回転するか、回転してから、足し算とスカラー倍をするか、結果は同じになる。これが写像の線形性である。言い換えると、ベクトル v1 と v2 の写像による行き先を知っていれば、第3のベクトル c1v1 + c2v2 の行き先が判ってしまう。平面上のベクトルは無限個あるが、それらは、適当な2つのベクトルから足し算とスカラー倍で作ることができる。したがって、写像が線形であれば、2つのベクトルについての情報からすべてのベクトルに対する情報が読み取れる。これが線形性のポイントなのである。
函数を調べる際にも線形性は必要となる。2変数の函数を考えよう。点 P0 = (x0, y0) の近くで函数 f(x, y) を微分するとは、函数を P = (x, y) が P0 の近くにあるときに、P0 からの微小変化∆xx = x-x0, ∆xy = y-y0 の1次式c1∆xx+c2∆xyで近似することである。
f(x, y) − f (x0, y0)∼ c1∆x+ c2∆y
c1 と c2 を与えるだけでこの1次式は決まる。微分することによって、無限個の情報の中から、P の近くでの函数の変化の様子を統制する、2個の量 c1, c2 を取り出すのである。
一定の性質を持つ函数の全体を線形空間として考えることも重要である。函数に対して和とスカラー倍が自然に定義されるが、線形の微分方程式の解の基本性質は解の全体が線形空間になることである。すなわち、2つの解から一次結合(足し算とスカラー倍で作ったベクトル)によって別の解を作ることができる。後で述べるように線形の微分方程式は自然現象の理解のために欠かせないものである。
量子力学では、物理状態はある線形空間 F のベクトルで表わされる。さらに、ハミルトニアンと呼ばれる線形写像 H : F → F があって、ある実数 E に対して Hv = Ev が成り立つようなベクトルのことを、エネルギーが E の状態と考える。量子力学では、線形代数は、理論そのものを記述する上で本質的な役割を演じるのである。
他科目・他分野との繋がり
全学共通科目には、多くの数学科目が提供されているが、それらは独立に存在するものではなく、互いに密接に関連している。微分積分は微分積分学 A,B で、線形代数は線形代数学 A,B で学ぶ。ここでは、それ以外の主要なものについて、その内容と互いの関係を概説しておく。
現象は函数で記述されると冒頭で述べたが、諸科学に現れる現象は「法則」に束縛されて生じる。例えば物理現象は該当する物理法則の下に出現する。現象を函数で記述したとき、物理法則は函数を束縛するが、多くの場合それは微分方程式という形で現れる。したがって、微分方程式は実際に現象を理解する上で重要な位置を占め、それを解くことは切実な問題である。例えば熱の伝導は、熱が温度の高い場所から温度の低い場所へ、温度勾配に比例して伝わるという原理と、温度の変化は流れ込む熱量に比例するという原理によって決まる。この2つの原理から、温度変化を表わす函数に対する方程式が導かれる。これは熱方程式と呼ばれる。熱方程式は線形微分方程式と言って解の全体が線形空間になるという性質を持つ。特に、細い針金の両端を温度 T1 と T2 に保ち、十分時間がたって温度変化がなくなった状態で、針金の各点における温度 T (x) は、位置 x の函数として線形微分方程式を満たすが、この場合の解は2つの函数 1 と x の一次結合(すなわち解は x の1次式)になる。これにより、T (x) =c1+c2 xの具体形が2個の未知数c1,c2に対する2元連立方程式(中学の数学)を解くことによって求まってしまう。微分方程式の初歩については、微分積分学及び線形代数学の知識を前提にして微分積分学続論 IIで学ぶ。
少々脱線にはなるが、微分方程式という言葉を出した以上、ニュートン力学に触れないわけにはいかない。ニュートンの運動方程式は最も有名な微分方程式である。 個別の力学現象に対し運動方程式を立て、それを微分積分の技法を使って解くことにより理解する。この意味で微分積分の技法は古典力学の問題に力を発揮するが、 それは偶然ではない。そもそも、ニュートンは古典力学を記述し、その問題を解くために微分積分学の着想に至ったのだから。
ベクトル場に対しては、一味違った「微分・積分」が導入される。その「微分」は「流れ」の局所的な傾向を記述し、「積分」は「流れ」の大局的な影響を記述するのに本質的な役割を演じる。さらに、ベクトル場に対する「微分積分学の基本定理」も確立されており、ガウスの発散定理やストークスの定理という名前で呼ばれる。これらは微分積分学続論 Iで学ぶベクトル解析の内容である。この科目も、微分積分学のみならず、線形代数の内容を前提として学ぶこととなる。
ベクトル解析は、電磁気学と相性が良く、電磁気学を記述するには必要不可欠なものである。実は、電磁気学を記述するためにベクトル解析が作られたという背景もあり、結果的に相性が良いのではなくそのように作られていると言うべきである。 電磁気学の理解とベクトル解析は不可分なのである。
以上、各科目の大まかな内容と分野間のつながりについて述べた。全学共通科目として提供される各数学科目はそれぞれが独立した一科目として提供されているのではなく、互いに関係しながら体系として積み上がっていくものだということがわかっていただけたであろうか。
おわりに
現在の数学は一つの学問として相当に洗練されおり、その体系は、広範な応用を念頭において「抽象的」に記述され、また誰にでも同じ内容が伝わるようにと、論理的な「厳密性」をもって組み立てられている。しかし、そのせいで初学者はしばしば全体像を見失うこともある。そんなときは、先に指摘したように各数学科目は繋がりをもっていることを思い出して欲しい。抽象性・厳密性ゆえに、学んでいる数学と自身の興味のある科学分野との関連が見えず、「為にする数学」をやっているように感じるときもあるかもしれない。そんなときにも、例えば「微分方程式と力学」や「ベクトル解析と電磁気学」のように、数学が現象の記述を目的に生まれたことを思い出してほしい。これらの視点が、学ぶことに疲れてしまったときに元気を与えてくれることもあるだろうから。
数学の理論と技法を身につけるためには、何よりも自分で手を動かして、実例に当たってみるべきである。他の自然科学において実験が重要であるように、数学においては演習が重要である。演習とは自分で考え、計算することでなければならない。そうして、納得のいかないことが出てきたときは、さらに考え、友だちと議論し、TA(ティーチングアシスタント)に教えてもらったり、先生に質問をする。繰り返しになるが、数学は数学の内部で、また他の自然科学との間で、強力なつながりを持っている。何かが解らないときに、そこに立ち止まらずに学習していくと、他とのつながりを見つけることによって、解らなかったことが解るようになることがある。解らないこと、納得のいかないことがあっても、その疑問を持ち続けて、あきらめずに先に進むことが大切である。
数学は潜在的には皆さんの将来の学問分野の基礎となる力を持っている。それを超えて皆さんによって数学が現実的に諸科学の基礎として活用されることを願う。





